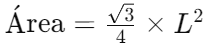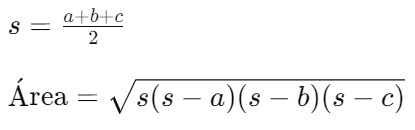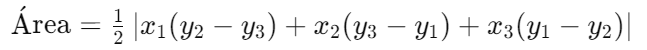Como Calcular a Área de Figuras Geométricas: Fórmulas e Exemplos

O cálculo da área de figuras geométricas é uma das habilidades matemáticas fundamentais, tanto em ambientes acadêmicos quanto na vida cotidiana.

Entender como calcular a área de figuras geométricas é essencial para resolver problemas relacionados a diversas áreas, como arquitetura, engenharia, design, e até em situações do dia a dia, como determinar a quantidade de tinta necessária para pintar uma parede ou o tamanho de um terreno.

O Que É Área?

A área é uma medida que expressa a extensão de uma superfície bidimensional. Em termos simples, ela nos diz o tamanho de uma superfície, seja ela plana, como uma folha de papel, ou a superfície de um objeto tridimensional, como a base de um cilindro.

A área é geralmente medida em unidades quadradas, como metros quadrados (m²), centímetros quadrados (cm²), ou quilômetros quadrados (km²), dependendo da escala da figura em questão.

A Importância do Cálculo de Área

Saber como calcular a área de figuras geométricas é crucial porque permite realizar estimativas e medições precisas em projetos de construção, planejamento urbano, agricultura e até na ciência.

Por exemplo, ao planejar a construção de uma casa, calcular a área de cada cômodo é necessário para determinar a quantidade de materiais que será utilizada.

No design, calcular a área permite criar projetos que otimizam o uso do espaço, garantindo funcionalidade e estética.

Conceitos Fundamentais

Para calcular a área de figuras geométricas, é importante entender alguns conceitos básicos:

• Unidade de Medida: A escolha da unidade de medida depende do contexto do problema. Para áreas menores, é comum usar centímetros quadrados ou metros quadrados. Para áreas maiores, como terrenos, utilizam-se hectares ou quilômetros quadrados.
• Figuras Simples vs. Figuras Complexas: Figuras simples, como quadrados, retângulos e círculos, possuem fórmulas diretas para o cálculo da área. Figuras complexas podem exigir a divisão da figura em partes menores e mais simples, cujas áreas são somadas para obter a área total.
• Fórmulas Específicas: Cada tipo de figura geométrica tem uma fórmula específica para o cálculo da área. Por exemplo, a área de um quadrado é calculada multiplicando a medida do lado por ele mesmo, enquanto a área de um círculo é calculada usando a fórmula πr², onde r é o raio do círculo.

A Base para Avançar em Cálculos Mais Complexos

Dominar os conceitos básicos para calcular a área de figuras geométricas é o primeiro passo para resolver problemas mais complexos, como o cálculo da área de figuras compostas ou irregulares.

Com uma compreensão sólida desses fundamentos, é possível avançar para tópicos mais desafiadores e aplicar esses conhecimentos em diferentes áreas do conhecimento e da prática profissional.

Fórmulas Essenciais para Calcular a Área das Principais Figuras Geométricas

Quando se trata de calcular a área de figuras geométricas, o uso de fórmulas específicas para cada tipo de figura é indispensável.

Essas fórmulas são aplicadas em diversas situações práticas, desde problemas simples de geometria até cálculos mais avançados em engenharia e arquitetura.

A seguir, vamos explorar as fórmulas essenciais para calcular a área das principais figuras geométricas, facilitando a resolução de problemas e a aplicação desses conceitos em diferentes contextos.

Área do Quadrado

O quadrado é uma figura geométrica com quatro lados iguais, o que torna seu cálculo de área bastante simples. A fórmula é:

Fórmula:

Área do Quadrado=L²

Onde:

Exemplo: Se um quadrado tem lados de 5 cm, sua área será:

Área=5²=25cm²

Área do Retângulo

O retângulo, assim como o quadrado, é uma figura com quatro lados, mas seus lados opostos são de comprimentos diferentes.

A fórmula para calcular a área é:

Fórmula:

Área do Retângulo=L×W

Onde:

• L é o comprimento do retângulo.
• W é a largura do retângulo.

Exemplo: Para um retângulo com comprimento de 8 cm e largura de 3 cm, a área será:

Área=8×3=24cm²

Área do Triângulo

O triângulo é uma figura com três lados, e sua área é calculada com base na medida da base e da altura. A fórmula é:

Fórmula:

Área do Triangulo=B×H/2​​

Onde:

• B é a base do triângulo.
• H é a altura, que é a distância perpendicular da base até o vértice oposto.

Exemplo: Se a base de um triângulo é 10 cm e sua altura é 6 cm, a área será:

Área=10×6/2​=30cm²

Área do Círculo

O círculo é uma figura geométrica que possui uma área calculada com base em seu raio, utilizando a constante π (pi), que é aproximadamente 3,14159.

A fórmula é:

Fórmula:

Área do Círculo=π×r²

Onde:

• r é o raio do círculo.

Exemplo: Para um círculo com raio de 7 cm, a área será:

Area=π×7²=π×49≈153,94cm²

Área do Trapézio

O trapézio é uma figura geométrica com dois lados paralelos de comprimentos diferentes, chamados de bases maior e menor. A fórmula para calcular a área é:

Fórmula:

Área do Trapézio=(B1​+B2​)×H/2​​

Onde:

• B₁ é a base maior do trapézio.
• B₂ é a base menor do trapézio.
• H é a altura, a distância perpendicular entre as bases.

Exemplo: Para um trapézio com bases de 8 cm e 5 cm, e altura de 4 cm, a área será:

Área=(8+5)×4/2​=52/2​=26cm²

Área do Losango

O losango é uma figura geométrica com quatro lados de mesmo comprimento, e sua área é calculada a partir das diagonais. A fórmula é:

Fórmula:

Área do Losango=D1​×D2/2​​​​

Onde:

• D₁ e D₂ são as diagonais do losango.

Exemplo: Para um losango com diagonais de 10 cm e 6 cm, a área será:

Área=10×6​/2=30cm²

Área do Paralelogramo

O paralelogramo, que inclui figuras como o retângulo e o losango, possui uma área calculada de forma semelhante ao retângulo. A fórmula é:

Fórmula:

Área do Paralelogramo=B×H

Onde:

• B é a base do paralelogramo.
• H é a altura.

Exemplo: Para um paralelogramo com base de 12 cm e altura de 5 cm, a área será:

Área=12×5=60cm²

Conclusão: A Importância de Conhecer as Fórmulas

Dominar essas fórmulas essenciais para calcular a área de figuras geométricas é vital não só para resolver problemas matemáticos, mas também para diversas aplicações práticas.

Seja no planejamento de um projeto de construção, na resolução de questões acadêmicas, ou em situações cotidianas, saber como aplicar essas fórmulas garante precisão e eficiência em cálculos que envolvem superfícies e espaços.

Área do Quadrado e Retângulo: Cálculos Simples e Práticos

O cálculo da área do quadrado e do retângulo é uma das primeiras lições de geometria aprendidas na escola, devido à simplicidade e à vasta aplicação prática dessas figuras no cotidiano.

Entender como realizar esses cálculos de maneira eficiente é essencial para diversas tarefas, como a determinação de espaços em projetos arquitetônicos, a escolha de materiais de construção, e até mesmo o planejamento de jardins ou ambientes internos.

Área do Quadrado

O quadrado é uma figura geométrica que possui quatro lados iguais, o que torna o cálculo da sua área muito direto e fácil de entender.

A fórmula para calcular a área de um quadrado é bastante simples:

Fórmula:

Área do Quadrado=L²

Onde:

• L é o comprimento de um dos lados do quadrado.

Exemplo Prático: Calculando a Área de um Quadrado

Suponha que você queira calcular a área de um quadrado cujo lado mede 6 metros. Usando a fórmula acima, o cálculo seria:

$Área=6²=36\text{m²}$

Isso significa que a área total do quadrado é de 36 metros quadrados. Este cálculo é útil em diversas situações, como ao planejar o espaço para a instalação de pisos em uma sala quadrada.

Aplicações Práticas do Cálculo de Área do Quadrado

• Planejamento de Espaços Internos: Ao decorar ou reformar um cômodo quadrado, calcular a área é necessário para determinar a quantidade de materiais como pisos, tapetes ou tintas.
• Agricultura e Paisagismo: No planejamento de hortas ou jardins quadrados, calcular a área ajuda a determinar o número de plantas que podem ser cultivadas em um determinado espaço.

Área do Retângulo

O retângulo, assim como o quadrado, é uma figura geométrica com quatro lados, mas com a diferença de que possui dois pares de lados opostos iguais.

O cálculo da área do retângulo é tão simples quanto o do quadrado, mas envolve duas dimensões diferentes: o comprimento e a largura.

Fórmula:

Área do Retângulo=L×W

Onde:

• L é o comprimento do retângulo.
• W é a largura do retângulo.

Exemplo Prático: Calculando a Área de um Retângulo

Vamos supor que você queira calcular a área de um retângulo com um comprimento de 8 metros e uma largura de 4 metros. O cálculo seria:

Área=8×4=32m²

Portanto, a área total desse retângulo é de 32 metros quadrados. Esse tipo de cálculo é comum em situações como a determinação do tamanho de um terreno ou a área disponível para construção.

Aplicações Práticas do Cálculo de Área do Retângulo

• Construção Civil: No planejamento de edifícios, calcular a área dos retângulos formados pelas paredes e pisos é essencial para o orçamento de materiais e a determinação do espaço disponível.
• Design de Interiores: Para otimizar o uso do espaço em um ambiente retangular, como uma sala ou escritório, é importante conhecer a área total para a disposição de móveis e decoração.

Comparação e Relações Entre o Quadrado e o Retângulo

Embora o quadrado seja um tipo especial de retângulo (onde todos os lados são iguais), a fórmula para calcular a área de ambos segue o mesmo princípio: multiplicar as duas dimensões principais.

No quadrado, ambas as dimensões são iguais, enquanto no retângulo, elas podem diferir. Essa simplicidade torna o cálculo de áreas dessas figuras uma ferramenta versátil e amplamente aplicável.

Como Calcular a Área do Triângulo: Entendendo as Fórmulas

O triângulo é uma das figuras geométricas mais fundamentais, presente em diversas áreas do conhecimento, desde a matemática básica até a arquitetura e a engenharia.

Calcular a área de um triângulo é uma habilidade essencial para quem lida com geometria, e entender as diferentes fórmulas disponíveis é crucial para resolver uma ampla gama de problemas práticos e teóricos.

Neste tópico, vamos explorar as principais fórmulas para calcular a área de um triângulo, explicando passo a passo como e quando usá-las.

Conceito Básico de Área do Triângulo

A área de um triângulo é a medida da superfície ocupada por essa figura geométrica de três lados. Para calcular essa área, é necessário conhecer algumas dimensões específicas do triângulo, como a base e a altura, ou, em casos mais complexos, os comprimentos dos lados.

Fórmula Básica para Calcular a Área do Triângulo

A fórmula mais comum e direta para calcular a área de um triângulo é baseada na medida da base e da altura:

Fórmula:

Área=B×H/2​

Onde:

• B é a base do triângulo.
• H é a altura, que é a distância perpendicular entre a base e o vértice oposto.

Exemplo Prático: Calculando a Área de um Triângulo Simples

Imagine que você tem um triângulo com uma base de 10 metros e uma altura de 5 metros. Usando a fórmula básica, o cálculo da área seria:

Área=10×5/2​=50/2​=25m²

Isso significa que a área do triângulo é de 25 metros quadrados. Este tipo de cálculo é frequentemente utilizado em situações como a medição de terrenos ou na criação de elementos decorativos triangulares.

Área de um Triângulo Equilátero

Um triângulo equilátero é um tipo especial de triângulo onde todos os lados têm o mesmo comprimento e todos os ângulos internos são de 60 graus.

Para calcular a área de um triângulo equilátero, você pode usar uma fórmula específica, baseada no comprimento de um dos lados:

Fórmula:

Onde:

• L é o comprimento de um dos lados do triângulo equilátero.

Exemplo Prático: Calculando a Área de um Triângulo Equilátero

Se um triângulo equilátero tem lados de 6 metros, a área será:

Essa fórmula é especialmente útil em situações de design e arquitetura onde figuras simétricas são utilizadas.

Fórmula de Herão: Área de um Triângulo com Três Lados Conhecidos

Quando conhecemos os comprimentos de todos os três lados de um triângulo, mas não a altura, podemos usar a Fórmula de Herão para calcular a área. Esta fórmula é bastante útil para triângulos irregulares.

Fórmula:

Onde:

• a, b, c são os comprimentos dos lados do triângulo.
• s é o semiperímetro do triângulo (a soma dos lados dividida por 2).

Exemplo Prático: Usando a Fórmula de Herão

Suponha que você tenha um triângulo com lados de 7 metros, 8 metros, e 9 metros. Primeiro, você calcula o semiperímetro:

A Fórmula de Heron é particularmente útil em geometria, quando não temos informações sobre a altura do triângulo, mas conhecemos todos os seus lados.

Cálculo de Área Usando Coordenadas: Triângulos em um Plano Cartesiano

Quando um triângulo é representado em um plano cartesiano com seus vértices definidos por coordenadas(x1​,y1​), (x2,y2) e (x3,y3), a área pode ser calculada usando uma fórmula específica:

Fórmula:

Essa fórmula é muito útil na geometria analítica e em problemas envolvendo triângulos definidos em sistemas de coordenadas.

Cálculo da Área de Figuras Circulares: Círculos e Esferas

Figuras circulares, como círculos e esferas, são fundamentais em várias áreas da ciência, engenharia, design e até na vida cotidiana.

Entender como calcular a área dessas figuras geométricas permite a aplicação precisa de conceitos em projetos, medições e análises.

Agora veremos as fórmulas essenciais para o cálculo da área de círculos e a superfície de esferas, explicando detalhadamente como utilizá-las em diferentes contextos.

Área do Círculo: Conceito e Fórmula Básica

O círculo é uma figura plana composta por todos os pontos equidistantes de um ponto central, conhecido como centro.

A medida da distância do centro até qualquer ponto na borda do círculo é chamada de raio (r). A área do círculo é a medida da superfície ocupada por essa figura geométrica e é calculada usando a seguinte fórmula:

Fórmula:

Área do Círculo=π×r²

Onde:

• r é o raio do círculo.
• π (pi) é uma constante matemática aproximadamente igual a 3,14159.

Exemplo Prático: Calculando a Área de um Círculo

Suponha que você tenha um círculo com um raio de 7 cm. Para calcular a área, substituímos o valor do raio na fórmula:

Área=π×7²=π×49≈153,94cm²

Portanto, a área desse círculo é de aproximadamente 153,94 cm². Este cálculo é amplamente usado em situações que variam desde a determinação do tamanho de mesas redondas até o cálculo da área de superfícies circulares em projetos de engenharia.

Perímetro do Círculo: Complemento Essencial

Além de calcular a área, muitas vezes é necessário determinar o perímetro (ou circunferência) de um círculo, especialmente em problemas que envolvem o comprimento de bordas ou a necessidade de cercar espaços circulares.

Fórmula para o Perímetro do Círculo:

Perímetro=2×π×r

Com o raio de 7 cm, o perímetro seria:

Perímetro=2×π×7≈43,98cm

A esfera é uma figura tridimensional onde todos os pontos da superfície estão à mesma distância do centro.

A área da superfície de uma esfera é uma medida importante em campos como física, astronomia, e engenharia mecânica, onde a forma esférica é comum. A fórmula para calcular a área da superfície de uma esfera é:

Fórmula:

Área da Superfície da Esfera=4×π×r²

Onde:

• r é o raio da esfera.

Exemplo Prático: Calculando a Área da Superfície de uma Esfera

Imagine que você precisa calcular a área da superfície de uma esfera com um raio de 10 cm. Usando a fórmula, o cálculo seria:

Área=4×π×10²=4×π×100=400×π≈1256,64cm²

Assim, a área da superfície dessa esfera é de aproximadamente 1256,64 cm². Este tipo de cálculo é fundamental, por exemplo, no design de objetos esféricos como bolas de esporte, reservatórios, e em estudos de física sobre corpos esféricos.

Área da Superfície de um Segmento Esférico

Um segmento esférico é a parte de uma esfera cortada por um plano. Para calcular a área da superfície de um segmento esférico, usa-se uma fórmula mais complexa, que considera tanto o raio da esfera quanto a altura do segmento (h):

Fórmula:

Área do Segmento Esférico=2×π×r×h

Onde:

• r é o raio da esfera.
• h é a altura do segmento.

Exemplo Prático: Cálculo para um Segmento Esférico

Suponha que você tenha um segmento esférico com um raio de 10 cm e uma altura de 5 cm. A área da superfície do segmento seria:

Área=2×π×10×5=100×π≈314,16 cm²

Aplicações Práticas do Cálculo de Áreas de Figuras Circulares

• Engenharia Civil e Arquitetura: Cálculos de áreas de círculos e esferas são fundamentais em projetos de infraestrutura, como estradas, pontes, e em construções que envolvem superfícies curvas.
• Astronomia e Física: No estudo de planetas, estrelas e partículas subatômicas, as áreas de esferas são usadas para entender fenômenos naturais e calcular grandezas físicas.
• Design e Fabricação de Produtos: Objetos esféricos, como bolas, recipientes e dispositivos ópticos, requerem cálculos precisos de área para garantir a funcionalidade e estética.

Entendendo a Fórmula da Área do Círculo: Pi e Seus Usos

O cálculo da área de um círculo é um dos conceitos mais fundamentais na geometria. A fórmula usada para encontrar a área de um círculo envolve uma constante matemática conhecida como π (pi).

Entender o papel do π e como ele é aplicado na fórmula da área do círculo é crucial para resolver uma ampla gama de problemas geométricos e práticos.

O Que é Pi (π)?

O π (pi) é uma constante matemática que representa a razão entre a circunferência de qualquer círculo e o seu diâmetro.

Essa razão é a mesma para todos os círculos, independentemente do seu tamanho, e é aproximadamente igual a 3,14159.

O valor de π é irracional, o que significa que suas casas decimais se estendem infinitamente sem repetir um padrão.

A Fórmula da Área do Círculo

A fórmula básica para calcular a área de um círculo é:

Area=π×r²

Onde:

• r é o raio do círculo, ou seja, a distância do centro até qualquer ponto na borda do círculo.
• π (pi) é a constante mencionada acima, com um valor aproximado de 3,14159.

Por Que Pi é Essencial?

O uso de π na fórmula da área do círculo é essencial porque ele conecta a geometria do círculo com suas propriedades naturais.

Como π está relacionado à circunferência e ao diâmetro, ele surge naturalmente quando calculamos a área da superfície delimitada por um círculo. Sem π, a fórmula não poderia refletir a verdadeira natureza geométrica do círculo.

Aplicações de Pi no Mundo Real

O π não é apenas uma curiosidade matemática; ele tem aplicações práticas em diversas áreas:

• Engenharia e Construção: Cálculo de áreas de terrenos circulares, dimensões de componentes mecânicos circulares, etc.
• Astronomia: Cálculo de áreas de planetas e outros corpos celestes.
• Design de Produtos: Projetos que envolvem formas circulares, como rodas, lentes, e mesas.

Curiosidades sobre Pi

• Dia do Pi: Celebrado em 14 de março (3/14, que se refere aos primeiros três dígitos de π).
• História: O valor de π foi conhecido e utilizado por várias civilizações antigas, incluindo os egípcios e os babilônios.

Exemplo Prático: Calculando a Área de uma Pizza

O cálculo da área de uma pizza é um exemplo prático de como a fórmula da área do círculo pode ser aplicada no dia a dia.

A área de uma pizza determina o quanto de massa, molho, queijo e outros ingredientes é necessário para cobrir sua superfície.

Esse cálculo pode ser útil para comparar o tamanho de pizzas e decidir qual oferece o melhor custo-benefício.

Passo a Passo para Calcular a Área de uma Pizza

Imagine que você tenha uma pizza de tamanho grande com um raio de 20 cm. Para calcular a área dessa pizza, você usaria a fórmula da área do círculo:

Área=π×r²

Substituindo o valor do raio:

Área=π×20²=π×400≈1256 cm²

Portanto, a área dessa pizza é de aproximadamente 1256 cm². Esse valor representa toda a superfície da pizza que será coberta pelos ingredientes.

Comparando Tamanhos de Pizzas

Se você quiser comparar essa pizza com uma pizza média, por exemplo, que tenha um raio de 15 cm, o cálculo da área seria:

Área=π×15²=π×225≈706,5 cm²

A pizza grande tem uma área significativamente maior que a pizza média, o que pode justificar uma diferença de preço.

Aplicações Práticas

• Planejamento de Festas: Saber calcular a área de uma pizza pode ajudar a planejar quantas pizzas são necessárias para alimentar um certo número de convidados.
• Decisões de Compra: Comparar áreas pode ajudar a determinar qual pizza oferece o melhor valor pelo preço, especialmente quando as pizzas têm tamanhos diferentes.

Curiosidades

• Pizza Gigante: Em competições, o cálculo da área é essencial para determinar recordes, como o maior tamanho de pizza já feito.
• Pizza em Pedaços: Dividindo a área total pela quantidade de fatias, você pode calcular a área de cada fatia e avaliar a proporção de massa e cobertura.

Como Calcular a Área de Figuras Complexas: Passo a Passo Detalhado

Dividindo Figuras Complexas em Partes Simples

Calcular a área de figuras complexas pode parecer uma tarefa desafiadora à primeira vista. No entanto, uma das estratégias mais eficazes para lidar com essa complexidade é dividir a figura em partes mais simples, cujas áreas podem ser calculadas individualmente.

Este método facilita o processo e permite que até mesmo formas irregulares sejam abordadas de maneira sistemática.

Identificando Partes Simples na Figura

O primeiro passo para dividir uma figura complexa é identificar formas geométricas básicas dentro dela. Estas formas podem incluir:

• Triângulos
• Retângulos
• Quadrados
• Círculos
• Trapézios

Ao reconhecer essas formas dentro de uma figura maior, você pode quebrar a figura original em partes que são mais fáceis de manejar.

Como Dividir a Figura

Dividir uma figura complexa pode ser feito de diferentes maneiras, dependendo da sua geometria. Algumas abordagens comuns incluem:

• Linhas de corte: Traçar linhas imaginárias que dividem a figura em formas simples. Por exemplo, um polígono irregular pode ser dividido em uma série de triângulos.
• Sobreposição de figuras: Enxergar a figura complexa como a soma de figuras mais simples que se sobrepõem, calculando suas áreas e subtraindo ou somando conforme necessário.

Cálculo das Áreas Individuais

Após dividir a figura, o próximo passo é calcular a área de cada parte individualmente. Utilize as fórmulas conhecidas para cada tipo de figura:

• Área de um triângulo: Área=b×h/2​
• Área de um retângulo ou quadrado: Área=l×c
• Área de um círculo: Área=π×r²
• Área de um trapézio: Área=(B+b)×h/2​

Somando as Áreas

Finalmente, some as áreas de todas as partes simples para obter a área total da figura complexa. Se alguma parte da figura foi subtraída (como um recorte ou um espaço vazio), lembre-se de subtrair a área correspondente.

Aplicações Práticas

Este método é amplamente utilizado em várias disciplinas, como:

• Engenharia e Construção: Para calcular áreas de terrenos irregulares ou superfícies não convencionais.
• Design Gráfico: Para determinar o espaço ocupado por elementos complexos em uma composição.
• Matemática e Educação: Como uma ferramenta didática para ensinar a resolução de problemas geométricos.

Exemplo Prático: Área de um Polígono Irregular

Agora que entendemos o processo, vamos aplicar esse conhecimento em um exemplo prático.

Exemplo: Polígono Irregular

Imagine que você tem um polígono irregular com cinco lados, onde é difícil aplicar uma fórmula direta para calcular a área. Para resolver isso, seguimos os passos descritos acima.

Passo 1: Divisão do Polígono

Neste exemplo, dividimos o polígono em três triângulos e um trapézio. Vamos considerar as medidas de cada figura:

• Triângulo 1: Base = 5 cm, Altura = 4 cm
• Triângulo 2: Base = 7 cm, Altura = 3 cm
• Triângulo 3: Base = 6 cm, Altura = 5 cm
• Trapézio: Base maior = 8 cm, Base menor = 4 cm, Altura = 3 cm

Passo 2: Cálculo das Áreas

• Área do Triângulo 1: Área=5×4/2=10 cm²
• Área do Triângulo 2: Área=7×3/2=10,5 cm²
• Área do Triângulo 3: Área=6×5/2=15 cm²
• Área do Trapézio: Área=(8+4)×3/2=18 cm²

Passo 3: Somando as Áreas

Finalmente, somamos todas as áreas para obter a área total do polígono irregular:

Área total=10cm²+10,5cm²+15cm²+18cm²=53,5cm²

Erros Comuns ao Calcular a Área e Como Evitá-los

Calcular a área de figuras geométricas é uma habilidade essencial tanto em contextos acadêmicos quanto práticos.

No entanto, erros podem facilmente ocorrer durante o processo, levando a resultados incorretos que podem impactar decisões importantes em áreas como engenharia, arquitetura e design.

Neste tópico, abordaremos os erros comuns ao calcular a área de figuras geométricas e ofereceremos dicas para evitá-los, garantindo que seus cálculos sejam precisos e confiáveis.

Erros Comuns ao Calcular a Área

1. Uso Incorreto das Fórmulas

Um dos erros mais comuns ao calcular a área de figuras geométricas é aplicar a fórmula errada para a figura em questão. Cada forma geométrica possui uma fórmula específica para calcular sua área.

Por exemplo, usar a fórmula da área do triângulo para calcular a área de um círculo resultará em um cálculo incorreto.

Como Evitar:

• Certifique-se de usar a fórmula correta para cada figura geométrica.
• Verifique se você tem a medida correta das variáveis necessárias para a fórmula (por exemplo, raio para círculos, base e altura para triângulos).

2. Erro na Medição das Dimensões

Medidas incorretas das dimensões, como raio, base ou altura, podem levar a erros significativos. Um pequeno erro na medição pode resultar em uma grande diferença na área calculada.

Como Evitar:

• Use ferramentas de medição precisas e verifique suas medidas duas vezes.
• Se possível, meça as dimensões várias vezes e use a média para obter uma medida mais precisa.

3. Unidades de Medida Incorretas

Confundir as unidades de medida ou não convertê-las corretamente é outro erro comum. Por exemplo, calcular a área usando centímetros em vez de metros pode levar a resultados incorretos se não forem convertidos adequadamente.

Como Evitar:

• Sempre verifique as unidades das medidas e converta-as para uma unidade comum antes de realizar os cálculos.
• Ao apresentar o resultado, use a mesma unidade de medida que foi utilizada nas medições.

4. Fórmulas Aplicadas Incorretamente

Aplicar a fórmula incorretamente, como esquecer de usar um fator divisor ou multiplicador, é um erro que pode ocorrer facilmente, especialmente em fórmulas mais complexas, como a área de um trapézio ou a superfície de uma esfera.

Como Evitar:

• Leia e entenda bem a fórmula antes de aplicá-la.
• Faça uma revisão cuidadosa dos cálculos e, se necessário, peça a alguém para revisar seu trabalho.

5. Não Considerar a Forma Completa

Ao calcular a área de figuras complexas, como polígonos irregulares, um erro comum é não considerar todas as partes da figura ou não dividir a figura corretamente em formas simples.

Como Evitar:

• Divida a figura complexa em formas geométricas simples e calcule a área de cada uma delas separadamente.
• Some todas as áreas calculadas para obter a área total da figura complexa.

Exemplos Práticos de Erros e Correções

Exemplo 1: Erro na Fórmula do Círculo

Erro: Calcular a área de um círculo usando a fórmula Área=2×π×r (fórmula do perímetro).

Correção: Use a fórmula correta: Área=π×r²

Exemplo 2: Medição Incorreta

Erro: Medir o raio de um círculo como 10 cm em vez de 15 cm, resultando em uma área muito menor.

Correção: Verifique e ajuste as medições antes de calcular a área.

Exemplo 3: Unidades de Medida

Erro: Calcular a área de um retângulo em metros quadrados quando as dimensões foram medidas em centímetros, resultando em um erro de conversão.

Correção: Converta todas as medidas para a mesma unidade antes de calcular a área e sempre verifique a unidade do resultado.

Dicas Adicionais para Precisão

• Verifique Sempre: Revise todos os cálculos e fórmulas aplicadas para garantir que não haja erros.
• Use Ferramentas Adequadas: Utilize calculadoras ou softwares específicos para cálculos geométricos quando possível.
• Entenda a Geometria: Compreender bem a geometria das figuras ajudará a evitar erros comuns e aplicar as fórmulas corretamente.

Considerações

Calcular a área de figuras geométricas é uma habilidade fundamental que une teoria e prática, essencial tanto para contextos acadêmicos quanto para aplicações do dia a dia.

Entender e aplicar corretamente as fórmulas para diferentes formas, como quadrados, triângulos, círculos e polígonos irregulares, não só facilita a resolução de problemas matemáticos, mas também é crucial em áreas práticas como construção, design e engenharia.

A precisão na medição, o uso adequado das fórmulas e a atenção às unidades de medida são aspectos chave para garantir cálculos corretos e eficazes.

Ao dominar essas técnicas, você pode aplicar seus conhecimentos de forma eficaz, garantindo que seus projetos e análises sejam baseados em dados precisos e confiáveis.