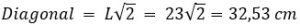Área de um Quadrado: Saiba como calcular e suas propriedades
A área do quadrado é utilizada na matemática básica e tem diversas aplicações no nosso cotidiano. Basicamente a área diz respeito ao tamanho da superfície da figura, sendo que no caso do quadrado será o tamanho da superfície dessa geometria. Além de muito cobrado na área de matemática, saber calcular a área de um quadrado pode ser considerado um conhecimento básico. Portanto, confira a seguir como fazer esse cálculo, a fórmula por trás e também alguns exemplos.
O quadrado
O quadrado é um quadrilátero regular, sendo formado por quatro lados que apresentam o mesmo comprimento, ou seja, que são congruentes. Outra propriedade do quadrado é que ele apresenta quatro ângulos retos, ou seja, que formam 90°. Portanto, a soma de todos os ângulos internos de um quadrado equivale a 360°.
Fórmula da área de um quadrado
A fórmula básica e mais conhecida de se calcular a área de uma figura é multiplicar a altura pelo comprimento ou base. O mesmo se aplica ao quadrado, em que se encontra a área multiplicando a medida de dois lados. No caso, como todos os lados são iguais, ou seja, a altura é igual a base, a fórmula da área de um quadrado é simplesmente dada por:
O = medida do lado.
Como todos os lados apresentam o mesmo valor, então a área seria o mesmo que pegar esse valor e elevar ele ao quadrado. Se a unidade de medida for centímetros então teremos a área dada em cm² e se for dada em metros teremos m². Que é o mesmo que multiplicar centímetro por centímetro e metro por metro.
Perímetro
Algo que pode confundir muitas vezes é o perímetro. Contudo, sempre tenha em mente que perímetro é diferente de área. A área é o tamanho da superfície enquanto o perímetro é a soma de todos os lados. A fórmula do perímetro é dada por:
Assim, a unidade de medida do perímetro será apenas centímetros (cm) ou metros (m) e não cm² ou m².
Diagonal do quadrado
Uma propriedade que também é importante e muito utilizada é a diagonal do quadrado. A diagonal é um segmento de reta que divide a figura em duas partes ao ligar dois vértices. Lembrando que a diagonal não liga dois vértices do mesmo lado. No caso do quadrado, a diagonal reparte a figura em dois triângulos retângulos, sendo que a mesma possui duas diagonais de mesmo valor (congruentes) que são perpendiculares, formando 90° uma com a outra.
Os triângulos retângulos são compostos por um ângulo reto, ou seja, de 90°, dois lados de mesmo comprimento e um lado maior. O lado maior é conhecido como hipotenusa, o lado oposto ao ângulo reto é chamado de cateto oposto e o lado adjacente ao ângulo é chamado de cateto adjacente.
A diagonal do quadrado pode ser encontrada por meio do Teorema de Pitágoras, cuja fórmula é dada por:
No caso a hipotenusa do triângulo seria a diagonal do quadrado. Como em um quadrado, temos que ambos os lados apresentam o mesmo comprimento, então podemos resumir a fórmula da diagonal para:
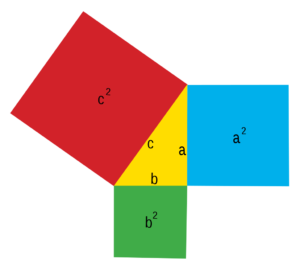
Teorema de Pitágoras
O teorema de Pitágoras: a soma das áreas dos quadrados construídos sobre os catetos (a e b) equivale à área do quadrado construído sobre a hipotenusa (c).
Assim, por meio da fórmula acima é possível encontrar o valor da diagonal apenas sabendo o valor de um lado do quadrado.
a2 = b2 + c2
Exemplos de como calcular a área de um quadrado
Exemplo 1: Como calcular a área de um Quadrado
Para um quadrado com um lado igual a 4 cm, qual será a área total do quadrado?
Pela propriedade do quadrado, sabemos que todos os lados são iguais, dessa forma temos um quadrado de 4 lados com comprimento de 4 cm cada um. Logo, sua área será de:
Exemplo 2: Como calcular a área de um Quadrado
Se um quadrado apresenta uma área de 225 cm², qual é o tamanho de cada um dos lados desse mesmo quadrado?
Nesse caso temos o problema inverso, ou seja, você tem o valor da área e quer saber o valor dos lados, para isso, basta substituir na fórmula aquilo que já se sabe:
Portanto, cada lado do quadrado tem um comprimento de 15 cm.
Exemplo 3: Como calcular a área de um Quadrado
Qual a diagonal de um quadrado cujos lados têm 5 cm de comprimento?
Pela fórmula obtida acima por meio do teorema de Pitágoras, sabemos que a diagonal será dada por:
Exemplo 4: Como calcular a área de um Quadrado
Um terreno tem 23 cm de comprimento em cada lado. Seu dono quer dividir o terreno em dois triângulos iguais e construir uma cerca ao redor de um desses triângulos. Quantos metros terá a cerca no total?
Se o terreno tem todos os lados com 23 cm, sabemos que se trata de um quadrado. Para saber o total de cerca que será usado, é preciso calcular o perímetro dessa figura e não a área. No caso teremos que somar: diagonal + lado + lado. Os comprimentos dos lados já sabemos, falta encontrar a diagonal. Para isso, basta substituir 23 cm na fórmula:
E então calculamos o perímetro:
Logo, a cerca terá um total aproximado de 78,53 cm.