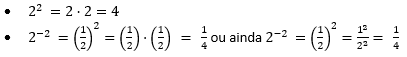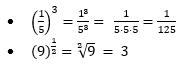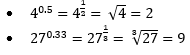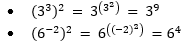Potenciação: tudo que você precisa saber
A potenciação é um método matemático para multiplicar vários números iguais, ou seja, você multiplica o próprio valor diversas vezes por ele mesmo. O número que será multiplicado é a base enquanto o expoente dele irá indicar quantas vezes ele irá se multiplicar. Além disso existem diversas condições e formas de utilizar a potenciação para facilitar os cálculos. Confira a seguir tudo sobre potenciação e como utilizar suas propriedades.
O que é potenciação?
Essa operação matemática, conhecida como potenciação ou exponenciação é usada para realizar a multiplicação do número por ele mesmo diversas vezes. Generalizando podemos escrever como
Como se utiliza essa operação?
Para utilizar essa operação basta saber como interpretar a potência, ou seja, identificar a base e o expoente. Veja os exemplos a seguir:
- 5³
Se lê como “cinco elevado a três” ou “cinco elevado à terceira potência”. Assim, 5 é a base e 3 o expoente. Dessa forma, a solução pode ser dada como a multiplicação do número cinco por ele mesmo três vezes. Matematicamente, temos que: 5³ = 5 x 5 x 5 = 125.
Nesse caso podemos identificar a base como sendo o número 8 e o expoente como o número 4. Assim, multiplicamos o número oito quatro vezes por ele mesmo. Dessa forma,
Condições e regras na potenciação
Existem algumas regras para que se possa utilizar esse método matemático e algumas condições que devem ser seguidas.
- Primeira condição: para que a potência exista a base deve ser diferente de zero.
- Segunda condição: sempre que o expoente for zero o resultado será um, independentemente do número utilizado como base. Por exemplo,
- Terceira condição: quando o expoente for igual a um, o resultado da potenciação será a própria base. Por exemplo, 2¹ = 2 .
Propriedades da potenciação
Dentro da potenciação existem uma série de propriedades que podem ser utilizadas para facilitar a resolução e rapidamente conseguir o resultado. Assim como alguns passos de como resolver corretamente, como por exemplo quando existe soma ou multiplicação de potências.
Potência com base positiva
Sendo diferente de zero é possível aplicar a potenciação, e quando a base for positiva o resultado também será positivo independentemente de o número no expoente ser ímpar ou par.
- 6² = 6 x 6 = 36: base positiva, expoente ímpar, resultado positivo
- 9³ = 9 x 9 x 9 =729: base positiva, expoente par, resultado positivo
Potência com base negativa
Quando a base da potenciação for negativa o resultado irá depender do expoente. Se o expoente for par, então o resultado será positivo pela regra negativo com negativo é igual a positivo. Já quando o expoente for ímpar então o resultado será negativo.
- (-6)² = (-6) x (-6) = +36 : base negativa, expoente par, resultado positivo
- (-6)³ = (-6) x (-6) x (-6) = -216: base negativa, expoente ímpar, resultado negativo
Observação: o negativo só será levado em conta na potenciação se ele estiver dentro dos parênteses. Caso não tenha os parênteses é como se o resultado da potenciação estivesse sendo multiplicado por menos um. Ou seja, (-6)² = +36 enquanto -6² = -36 .
Potência com expoente positivo ou negativo
Tirando as exceções acima de quando o expoente for zero ou um, as regras para expoente são simples. Se o expoente for positivo e diferente de um, a potência é resolvida normalmente. Se o expoente for negativo é preciso inverter a base para eliminar o negativo e então resolver a potenciação. Veja os exemplos abaixo:
Potenciação com fração
Para resolver potenciações que envolvam frações, temos dois casos: na base e no expoente. Se a fração for na base, basta distribuir os expoentes e resolver normalmente. Agora se a fração estiver no expoente é preciso transformar na raiz equivalente para então conseguir resolver.
Potenciação com decimal
Os números podem ser representados também na forma de decimais, ou seja, entre 0 e 1. Ao utilizar decimais na potenciação o primeiro passo para resolver é transformando o decimal em fração.
Multiplicação de potências de mesma base
Se ocorre uma multiplicação entre duas potências e elas tem a mesma base, isso é facilmente resolvido somando os expoentes e então calculando normalmente a potenciação.
Divisão de potências
Como a divisão é o inverso da multiplicação, ao invés de somarmos vamos subtrair os expoentes se ambas as bases forem iguais. Confira a seguir:
Potência de potência
Ainda pode haver casos em que uma potência está elevada a um expoente. A estratégia adotada nesse caso é resolver a potência do expoente e depois a potência da base. Confira a seguir os exemplos:
Conclusão
As potências são ótimas ferramentas matemáticas para simplificar certos cálculos e com algumas propriedades é possível tornar suas resoluções muito mais fáceis. Dessa forma, não deixe de aprender as diferentes propriedades da potenciação e não ter mais problemas ao resolver questões que envolvam essa temática.