Fração: O que é, Tipos, Operações com Frações, Exercícios
Certamente, você já deve ter ouvido falar a respeito das frações. Quando nos perguntamos do que se trata, devemos ter em mente que uma fração nada mais é que, uma forma de representar uma divisão em partes iguais.
Sendo assim, em uma fração, sempre temos dois números inteiros: número que sofrerá divisão e o número de partes em que será dividido. Esse sistema pode ser elaborado da seguinte maneira:
Vale lembrar que o número que sofre divisão é chamado de numerador, enquanto o número de partes é o denominador. Desse modo, o esquema aparece formalmente como:
É necessário sempre respeitar essa ordem obrigatória da fração. Além disso, existem algumas outras formas de representar uma fração, sendo as mais comuns:
Por isso, para transformar uma fração em um número, basta realizar o processo de divisão comum. No caso anteriormente exemplificado, o resultado fica:
4÷2=2
No caso, o número 2 é inteiro, mas nem sempre as frações chegam a esse tipo de resultado. A seguir, você conhecerá os 4 principais tipos de fração que podem ser encontrados.
Introdução às Frações:
Tipos de Fração
Própria
Podemos escolher quaisquer números inteiros para compor o numerador e o denominador de uma fração. Nessas dadas condições, quando o numerador é maior que o denominador, o resultado é um valor maior que zero e a fração é chamada de fração própria.
Exemplificando:
Imprópria
Trata-se de uma situação contrária a de uma fração própria. Nesse caso, o numerador é menor que o denominador, e a fração representa um número menor que zero. Assim, passa a ser chamada de fração imprópria.
Exemplificando:
Aparente
Uma fração aparente é aquela que, representa um número inteiro. Recebe esse nome pois é possível visualizar seu resultado mais facilmente, visto que o numerador é múltiplo (ou seja, aparece na tabuada) do denominador.
Exemplificando:
Equivalentes
Frações equivalentes são aquelas que, ainda que sejam representadas por números diferentes, fornecem o mesmo resultado. Isso acontece quando os números utilizados são proporcionais, ou seja:
Operações com frações
Como mencionado anteriormente, a fração é uma representação numérica e, por isso, também podemos realizar operações com frações. A seguir, ensinaremos como realizar as operações básicas, sendo elas: soma/adição e subtração.
Adição de Frações
Somar frações é o processo de unir partes. Sendo assim, para somar duas frações, é preciso que elas possuam o mesmo denominador. Por isso, existem dois tipos de soma de frações.
A) Com denominadores iguais
Depois de verificar que os denominadores são iguais, você deverá somar os numeradores e manter o denominador.
Exemplificando:
O resultado está pronto! Caso seja uma fração aparente como essa, você ainda pode inserir o resultado na forma de um número inteiro, nesse caso:
B) Com denominadores diferentes
Contudo, existem casos em que os denominadores não são iguais, sendo necessário encontrar frações equivalentes para que seja possível efetuar a soma. Desse modo:
Subtração de Frações
Na subtração, se aplicam as mesmas regras da adição. Contudo, em vez de somar, será necessário subtrair os numeradores, tal como uma subtração comum. Exemplificando:
A) Com denominadores iguais
 B) Com denominadores diferentes
B) Com denominadores diferentes
Confira aqui nosso artigo sobre divisão de frações.
Como se lê as frações?
A leitura de uma fração depende do seu denominador, podendo ser dividida em dois grupos.
O primeiro grupo compreende os denominadores iguais a 2, 3, 4, 5, 6, 7, 8, 9, 10, 100 e 1000
Primeiro se lê o numerador e em seguida seu denominador.
Três meios; Dois Sextos; Um décimo;
Um terço; Quatro sétimos; Oito centésimos;
Cinco quartos; Seis oitavos; Dois milésimos
Sete Quintos; Três nonos;
O segundo grupo compreende os denominadores que não pertencem ao primeiro, e acrescentamos a palavra AVOS
Sete quinze avos;
Treze cinquenta e sete avos;
Quarenta e cinco cento e oitenta e dois avos;
Sete vinte e um avos.
Para frações que tem como denominador o número um, lê-se apenas o numerador, pois essas frações são números inteiros.
Exercícios sobre Frações
Exercício 1: (UFMG 2009)
Paula comprou dois potes de sorvete, ambos com a mesma quantidade do produto.
Um dos potes continha quantidades iguais dos sabores chocolate, creme e morango; e o outro, quantidades iguais dos sabores chocolate e baunilha.
Então, é CORRETO afirmar que, nessa compra, a fração correspondente à quantidade de sorvete do sabor chocolate foi:
| 2/5 | |
| 3/5 | |
| 5/12 | |
| 5/6 |
Exercício 2: (UECE 2018.1 – 1ª Fase)
A soma de todas as frações da forma n/(n+1), onde n é um elemento do conjunto {1, 2, 3, 4, 5}, é
| 4,55. | |
| 6,55. | |
| 5,55. | |
| 3,55. |
Respostas:
1- C
2 -D
Aprenda mais sobre frações com este modulo introdutório
Gostou? Entendeu melhor? Compartilhe!





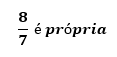





 B) Com denominadores diferentes
B) Com denominadores diferentes












