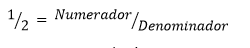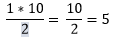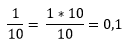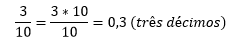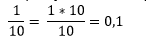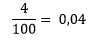Números Decimais: quem são, como entendê-los melhor e operá-los
Na matemática, os números decimais são representações de números fracionados, ou seja, números que não são inteiros, mas apresenta uma relação com a parte inteira.
Eles são separados dos números inteiros com o uso da vírgula e podem ser lidos de duas formas: ‘0,5’ – zero vírgula 5 – ou ‘1/2’ – meio. Quando observarmos o número como uma fração, obtemos algumas informações:
Dessa operação, chamada divisão, temos que o Numerador é menor que o Denominador, logo não há como ocorrer uma partição exata. Sendo assim, multiplicamos o numerador por uma potência de 10 e se verifica a possibilidade de ocorrer uma partição.
Encontrado o valor decimal, podemos então escrevê-lo como 0,5 e interpretá-lo como meio. Ou 5 décimos.
Por que décimos?
Quando queremos encontrar o algarismo decimal, buscamos calcular o fracionamento do número em partes iguais. Utilizando das regras da divisão, podemos concluir que a multiplicação por potências de 10 e o uso da vírgula, nos auxiliam na partição do numerador em quantidades iguais do denominador. E que a cada multiplicação por 10 efetuada é movido uma casa decimal para a direita após a vírgula.
Exemplo 1:
Explicação:
Quando efetuada a divisão 1 ÷ 10, há necessidade de multiplicar o numerador por 10 para que seja possível a partição, ocorrendo então o deslocamento da casa decimal após a vírgula. Dessa divisão, interpretamos que a divisão 1 ÷ 10 resulta no valor de 0,1 (um décimo).
Vamos agora entender o número 2,5:
Percebemos que ele possui 2 partes inteiras e, após a vírgula, o número 5 na casa decimal. Agora separamos os 2 números inteiros encontrados e vejamos apenas o 0,5, sendo possível interpretá-lo como meio, ou melhor, 5 décimos. Como trabalhado no exemplo anterior, podemos ver que na casa decimal ocorre a operação 5 ÷ 10.
E ainda, no cálculo de 5 ÷ 10 é utilizada a regra do fator comum que permite simplificar mais a operação. Ou seja, fatorando o Numerador e Denominador por um valor comum, como nesse caso o número 5, obtemos a divisão de 1/2.
Mais números e mais casas dos números decimais
Vamos fazer a leitura de mais alguns números:
- 1,3:
Já podemos começar afirmando que temos o número 1 na parte inteira (valor antes da vírgula) e que a casa decimal contém o número 3 (valor após a vírgula). Agora observando a parte decimal, encontramos a operação de divisão 3 ÷ 10:
Semelhante ao exemplo 1, quando efetuada a divisão, depara-se com o numerador menor que o denominador, sendo necessário então o uso da potência de 10 e da vírgula para assim conseguirmos realizar o cálculo da fração.
- 3,14:
Iniciamos fazendo a leitura da parte inteira igual a 3 e, após a vírgula, encontramos dois algarismos decimais. A partir da nossa observação da operação de divisão, para a primeira casa decimal, temos:
E para o segundo algarismo decimal – 4 – que está na segunda casa, lembramos que o deslocamento significa a inclusão de mais uma potência de 10, resultando então:
- 8,999:
Temos o número 8 na parte real e nos algarismos decimais, o número 9 se repetindo nas 3 casas existentes depois da virgula. Essas 3 casas nos mostram as seguintes operações:
Compondo então a parte decimal igual a 0,999
Posso somar ou subtrair esses números decimais?
Sim, as operações matemáticas de adição e subtração operam semelhantemente a tradicional, porém há mais algumas regras:
- A operação será sempre casa decimal com casa decimal e inteiro com inteiro, ficando assim a vírgula na mesma posição entre os dois números.
Exemplo 2:
Vamos operar os números 2,5 e 1,3. Em ambos notamos um número inteiro e uma casa decimal após a vírgula. Se iniciarmos com a adição dos números, temos que na casa decimal (3 + 5 = 8) e na parte inteira (1 + 2 = 3), resultando no número 3,8. Para a subtração, é subtraído o menor valor do maior valor e operado da mesma forma, casa decimal (5 – 3 = 2) e parte inteira (2 – 1 = 1), resultando em 1,2.
- As casas decimais são preenchidas por décimos e quando completos, se tornam um inteiro. Ou seja, na soma de 0,1 (um décimo) com 0,9 (nove décimos), teríamos a divisão de 10 ÷ 10 que resulta em 1, portanto 0,9 + 0,1 = 1,0 (um inteiro).
- E na subtração, caso não possuir números a serem subtraídos, o vizinho da esquerda doa 1 décimo da sua casa, sendo acrescentando então 10 décimos ao valor que será subtraído.
Exemplo 3:
Vamos subtrair do número 3,14 o número 1,3. Resumindo brevemente a primeira regra, colocamos vírgula embaixo de vírgula. Temos que em um dos números há duas casas decimais, o que nos obriga a acrescentarmos a segunda casa também no outro número, mas com o número 0, porque não há décimos na cada.
Podemos então calcular 3,14 – 1,30 como calculado acima, iniciando com o segundo algarismo decimal (4 – 0 = 4). Ao prosseguirmos para a o primeiro algarismo decimal, nos deparamos com 1 décimo sendo insuficiente para subtrair 3 décimos, nos obrigando a emprestar 10 décimos do vizinho da esquerda – o número 3. Nessa subtração agora temos (11 – 3 = 8).
Quando seguimos a subtração da última parte, a inteira, lembramos que o 3 emprestou 10 décimos de seu valor para a conta anterior, valendo agora 2 (perdeu 1 inteiro = 10 décimos). Por fim então, calculamos (2 – 1 = 1) para obtermos o valor da parte inteira e escrevemos o resultado como 1,84.
Então também posso multiplicá-los e dividi-los?
Sim, começamos com pela multiplicação, pois a regra é mais simples. Não há a necessidade de posicionarmos vírgula embaixo de vírgula, apenas realize a multiplicação completa. Quando obtido o resultado, retornamos aos números utilizados para a multiplicação e analisamos quantas potências de 10 estão contidas na operação que significará o deslocamento da vírgula número final.
Exemplo 4:
1,002 X 1,2:
1º Passo – Calculamos 1002 * 12 = 12024.
2º Passo – Temos no número ‘1,002’ três casas decimais e no número ‘1,2’ uma casa decimal, totalizando 4 potencias envolvidas na operação.
3º Passo – Reposicionamos então a vírgula 4 casas a esquerda gerando o resultado igual a 1,2024.
E para a divisão, é fundamental que os números possuam a mesma quantidade de casas decimais e caso não esteja representado na forma decimal, é necessário escrevê-lo com o uso da vírgula e zeros. Vamos ver mais na prática:
Exemplo 5:
15,3 ÷ 3:
1º Passo – Montamos o cálculo de 15,3 ÷ 3,0.
2º Passo – Dividindo a parte inteira 15 por 3, obtemos o resultado igual a 5, mas note que há um resto na divisão de 0,3.
3º Passo – Como aprendemos, usamos a vírgula e multiplicamos o resto por 10 afim de a divisão de 3,0 por 3,0, que resulta no valor 0,1.
4º Passo – Por fim reescrevemos o resultado da divisão como 5,1.
Pratique as operações com Números Decimais
- 2,1 + 2,0
- 2,4 – 2,12
- 2,1 * 2,22
- 2,2 ÷ 1,1
- 10,5 ÷ 5,25
- 48,4 ÷ 12,1
Gabarito
- 4,1
- 0,28
- 4,662
- 2,42
- 2,0
- 4,0