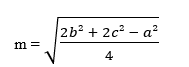Como calcular a mediana: O que é, calculo e exercícios
Você quer aprender, de forma simples, como calcular a mediana? Então está no lugar certo! Preparamos esse artigo para você aprender definitivamente como fazer esse cálculo.
É muito importante dominar esse tipo de conteúdo, isso porque é um dos assuntos mais cobrados em provas, como por exemplo, vestibulares e o ENEM.
Então, se você quer ficar craque em calcular a mediana, continue a leitura.
Você pode gostar de ler também:
O que é a mediana?
A mediana é classifica como uma medida da tendência central de um conjunto de números, sendo uma ferramenta muito utilizada para diminuir um conjunto de valores em apenas um. Dessa forma, tanto a mediana, quanto a moda e a média são consideradas medidas de posição.
Portanto, a palavra “mediana” se refere ao “meio”, ela exatamente indica o número central de uma coleção de valores números de uma determinada amostra.
Ainda, é importante ressaltar que os números referentes as informações, sejam colocadas em ordem seja decrescente ou crescente.
Assim, em casos onde haja números ímpares, a mediana se caracterizará como o valor central desse conjunto numérico. Agora, se for uma quantidade par de valores, é necessário calcular a média aritmética dos dois números centrais. E, dessa forma, o resultado da média aritmética será o valor da mediana.
Diferença entre media e mediana
A média é o valor resultante da somatória de todos os números de um determinado intervalo, dividido pela quantidade de números. Já a mediana é o número ou valor que fica exatamente no meio de um determinado intervalo de números
Fórmula da mediana
Para determinar o valor da mediana é imprescindível colocar os números em ordem decrescente ou crescente, como preferir.
Conjunto de valores par: quando o conjunto de valores for par, basta selecionar os dois valores centrais, soma-los de dividir por dois.
Conjunto de valores ímpar: quando o conjunto de valor for ímpar, basta selecionar o número central da sequência.
Como calcular a mediana
A seguir vamos trazer alguns exemplos de como calcular a mediana, veja:
- As notas de um aluno em um semestre do ensino médio, em ordem crescente, são: 4,0;4,0;5,0;7,0;7,0.
R: A mediana cujo valor está no centro da amostra, ou seja, 5,0. Portanto, podemos considerar que 40% das notas estão acima da nota 5,0 e os outros 40% estão abaixo da nota 5,0.
- A quantidade de hotéis 6 estrelas espalhados pelas cidades do litoral do estado de Santa Catarina é a seguinte: 1, 2, 3, 3, 5, 7, 8, 10, 10, 10.
R: Perceba que a amostra de dados possui dez valores (quantidade par) e, portanto, não existe um valor central. Assim, para calcular a mediana, nesse caso, deve-se calcular a média dos dois números centrais da sequência (5 e 7):
Mediana = 5 + 7 / 2
Mediana = 6
Como resposta, 50% das cidades pesquisadas tem mais de 6 hotéis seis estrelas e 50% das cidades pesquisas tem menos de 6 hotéis seis estrelas.
Como calcular a mediana de um gráfico
Para calcular a mediana de um gráfico, devemos colocar todos os valores da ordenada y do gráfico em ordem crescente. Depois encontrar a posição da mediana n, ou seja, quantos valores existem na ordenada y.
Usar a fórmula: n + 1 / 2 e descobrir o valor da mediana dos valores do gráfico.
Como calcular a mediana de um triangulo
Ainda, a mediana também pode ser determinada a partir dos dados de um triangulo. Dessa forma, a mediana é definida como sendo a reta que liga um vértice do triângulo na metade. Ou seja, o ponto médio da aresta oposta a esse triângulo.
Veja a seguir como funciona o cálculo da mediana de um triângulo.
Na figura acima temos representadas medianos do triângulo. Assim, os segmentos de reta AP, BN e CM são as três medianas desse triângulo.
Portanto, a mediana vai dividir o triângulo em outros dois triângulos menores, cujas áreas são iguais. divide qualquer triângulo em dois triângulos menores e de áreas iguais.
Para calcular o valor da mediana, podemos usar a seguinte fórmula:
No qual,
m é o tamanho da mediana
a é o lado do triângulo tocado pela mediana,
b e c são os demais lados do triângulo.
Exercícios com respostas sobre mediana
- Em uma escola de ensino fundamental, a professora de matemática pediu aos alunos que escrevessem suas alturas na lousa. As alturas foram as seguintes: 1,54 m; 1,57 m, 1,58 m; 1,61 m; 1,63 m; 1,63 m; 1,65m; 1,66 m e 1,68 m.
A partir desses valores, qual é a mediana de altura desses alunos?
- Calcule o valor da mediana da seguinte amostra de idade dos alunos de uma sala de Educação para Jovens e Adultos: 32, 27, 15, 44, 15, 32.
- Nos quatro primeiros dias úteis de uma semana o vendedor de uma loja de cosméticos atendeu 19, 15, 17 e 21 clientes. Porém, no quinto dia útil dessa mesma semana o vendedor atendeu n clientes.
Se a média do número clientes atendidos diariamente pelo vendedor nos cinco dias úteis dessa semana foi 19, a mediana foi de clientes atendidos foi:
- a) 16.
b) 19.
c) 17.
d) 23.
e) 21.
Respostas:
- 63m
- 29,5 anos
- B
Não esqueça de compartilhar esse artigo.