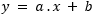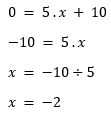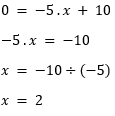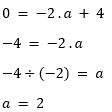Função do 1 grau: O que é, exemplos e exercícios
Hoje você vai aprender o que é uma função, exemplos de funções, o que é uma função de primeiro grau que é o mesmo que função afim, entre outros tópicos de matemática relacionados a função e equação.
Alguns tópicos que serão abordados são o que é função, função de primeiro grau, como encontrar o zero da função do 1 grau e como determinar uma função a partir de um gráfico. Confira!
O que é Função
Antes de começarmos a estudar a função de 1 º propriamente dita vamos entender o que é uma função. Uma função é uma relação entre dois conjuntos. Considere os números do conjunto A: 1,2,3,4 e 5. Eles podem estar relacionados aos números do conjunto B:2,4,6,8 e 10 através de uma função que pode ser, por exemplo B = 2 . A. Isso quer dizer que os valores de B é igual a multiplicar os valores de A por 2.
Em uma função é importante saber que existem algumas regras. Qualquer valor do conjunto A pode estar relacionado a um único valor do conjunto B, isso é, um único valor de A não pode estar associado a mais de um valor do conjunto B. Além disso podem existir valores de A para os quais não existam correspondentes em B e podem existir, também, dois ou mais valores distintos de A que estão relacionados a um único valor de B. Veja ambos os casos na prática.
Condições para definir uma função primeiro grau
Caso 1: Um valor de x não tem nenhum correspondente em y
Considere a função y=10/x (y é igual a 10 dividido por x)
Se considerarmos os valores de x:{0,1,2,5} e substituirmos na função y=10/x temos os valores de y:{∄, 10, 5 ,2 }.
Apenas a critério de exemplo para ficar mais claro:
Com x = 5, temos:
y = 10 / 5
y = 2
E assim para os demais. Como podemos perceber não existe valor de y, isso é representado pelo ∄, quando o valor de x é 0.
Caso 2: Dois valores distintos de x correspondem a um mesmo y
Considere a função y=x^2 (y é igual a x vezes x)
Se considerarmos os valores de x:{1,2, -2} e substituirmos na função y=x^2 temos os valores de y:{1, 4, 4}.
Apenas a critério de exemplo para ficar mais claro:
Com x = 2, temos:
y = 2 . 2
y = 4
Com x = -2, temos:
y = (-2) . (-2)
y = 4
E assim para os demais. Como podemos perceber um único valor de y pode corresponder a um ou mais valor de x.
ATENÇÃO: Para ser uma função não pode existir um único x que esteja relacionado a mais de um y.
Definido o que é função podemos começar a explicar o que é função de primeiro grau.
O que é Função de primeiro grau
O grau da função está relacionado ao maior número em que o x está elevado. Se o x está elevado a um a função é de primeiro grau.
No caso mais geral a função de primeiro grau é da forma:
Em uma função de primeiro grau o termo que multiplica fração o x é denominado coeficiente linear e no caso acima é o a. A letra b é denominada constante.
Observando, graficamente, variações de equação de primeiro grau
Se pensarmos em casos gerais e plotamos em um gráfico uma equação de primeiro grau podemos ter quatro possíveis combinações:
- a é positivo e b é positivo
- a é positivo e b é negativo
- a é negativo e b é negativo
- a é negativo e b é positivo
Confira o gráfico abaixo com os valores de x no eixo horizontal e os valores de y no eixo vertical.
Em vermelho, temos a função do 1ª grau
y = 5x + 10
Em azul, temos a função do 1ª grau
y = 5x – 10
Em verde, temos a função do 1ª grau
y = -5x – 10
Em roxo, temos a função de primeiro grau
y = -5x+ 10
Figura 1: Gráficos de funções variando os coeficientes e as constantes.
Como podemos ver os gráficos verdes e roxo são decrescentes, isso é, com o aumento do valor de x o y decai. Já os gráficos vermelho e azul são crescentes, isso é, o y aumenta se x aumenta. O que torna uma função de primeiro grau crescente ou decrescente é o valor se o valor de a é positivo ou negativo. Lembre-se:
Se a é positivo a função é crescente
Se a é negativo a função é decrescente
O valor de b pode ser utilizado para encontrar o local onde a função intercepta o eixo x. A intersecção da função com o eixo x acontece quando o valor de y é zero. Confira os dois exemplos abaixo para encontrar em qual valor de x existe a intersecção da função com o eixo x. Tal valor é denominado zero da função pois o y assume valor de 0.
Encontrando o zero de uma função de primeiro grau
Exemplo 1: y = 5x + 10
Note que nesse exemplo a = 5 e b = 10
A condição para encontrar a intersecção é que y = 0
Realiza a subtração do valor de b que é 10 de ambos os lados
Divide ambos os lados pelo valor de a que é 5
Quando x = -2 a função intercepta no eixo x.
Se observar a Figura 1 vai perceber que a função vermelha intercepta o eixo x, horizontal , quando o valor de x = -2.
Exemplo 2:y = -5x + 10
Note que nesse exemplo a = -5 e b = 10
A condição para encontrar a intersecção é que y = 0
Realiza a subtração do valor de b que é 10 de ambos os lados
Divide ambos os lados pelo valor de a que é -5
Quando x = -2 a função intercepta no eixo x.
Se observar a Figura 1 vai perceber que a função roxa intercepta o eixo x, horizontal , quando o valor de x = 2.
Encontrando os valores a e b através de um gráfico
É possível encontrar os valores a e b somente através do gráfico de uma função. Considere o gráfico com duas funções.
Exemplo A – função na cor preta
Existem várias técnicas para encontrar os valores de a e b de uma função do 1 grau. O valor de b é o mais fácil de ser encontrado pois ele é o que quando x = 0, ou seja, a função intercepta o eixo y. Sendo assim o valor de b é 4.
Já para encontrar o valor de a é necessário fazer alguns cálculos. O valor de a representa a inclinação da reta. Quanto maior o valor de a, maior a inclinação. Para encontrar a devemos utilizar valores de dois pontos. Como exemplo vamos utilizar os pontos x = -2 e y = 0, isto é, (-2;0)
4 é o valor que encontramos com b. X = -2 e Y = 0 foram os pontos tomados
Subtraímos o valor de b em ambos os lados da equação
Dividimos pelo valor de x que é -2
Encontramos o valor de a que é 2.
Exemplo B – função na cor vermelha
Como visto no exemplo anterior o valor de b para o caso da função na cor vermelha é 1 pois é o valor de y quando x = 0.
Para encontrar o valor de a escolhemos um ponto qualquer da função na cor vermelha. Vamos escolher o ponto de x = 2 e y = 2, isso é, (2;1)
1 é o valor que encontramos com b. X = 2 e Y = 2 foram os pontos tomados
Subtraímos o valor de b em ambos os lados da equação
Dividimos pelo valor de x que é 2
Encontramos o valor de a que é 0.5
Exercícios
Os exemplos 1 e 2 de encontrando o zero de uma função do 1 grau são casos de como resolver uma equação de primeiro grau, ou seja, encontrar o zero. As explicações ao lado dos exemplos vão te ajudar a resolver os seguintes exercícios de equação de primeiro grau para encontrar o zero:
- y = 2x+4
- y = 2x-4
- y = 3x+6
- y = -3x+6
- y = -9x-9
- y = -9x+18
- y = -36x+18
- y = 30x-60
Existem ainda exercícios mais elaborados que envolvem um enunciado. Resolva-os à seguir:
- Tiago era um homem que gostava de pescar. Sempre que pescava um peixe pesava e dizia que pescou um peixe com 3 quilos a mais do que o valor real. Sendo assim, se Tiago disse que pescou um peixe de 10 quilos, qual o peso real do peixe que Tiago pescou?
- Marina adora andar de bicicleta. Marina pedala uma distância conforme a equação Y = 5. x. O x é o dia da semana. Se é domingo x=1, se segunda, x=2, se terça, x=3 , e assim por diante. Quantos quilômetros Marina pedala no sábado?
- José é um colecionador de carros. Sempre que vende um carro vende pelo dobro do preço que comprou mais 10.000,00 reais. Se José vendeu um carro por 200.000,00 qual foi o valor que pagou no carro quando comprou?
Encontre os valores de a e b para as funções abaixo: