Como calcular MMC (Mínimo Múltiplo Comum)
Como calcular MMC (Mínimo Múltiplo Comum) – O Mínimo Múltiplo Comum, ou simplesmente MMC, é o resultado da operação de minimização, em que se pretende encontrar o menor valor que seja múltiplo comum de determinados números.
Em outras palavras, o MMC de dois ou mais números inteiros será o menor valor capaz de multiplicar todos os números desejados ao mesmo tempo, com exceção do zero.
Este processo é útil para realizar operações com frações, de modo que o denominador seja comum a todos os números durante o procedimento.
Exemplo Calcular MMC
Por exemplo, para calcular MMC de 2, 4 e 6 devemos realizar a seguinte operação, chamada de “fatoração simultânea”:
Divide-se os números desejados (8, 12) pelo menor número divisível entre eles, no caso, o número 2. Depois, realiza-se o processo novamente até não haver mais números que sejam divididos, conservando-se aqueles que não sejam.
Após, segue-se ao próximo número inteiro, no caso, 3, repetindo-se até que todos os números sejam fatorados a 1.
Veja abaixo como calcular MMC:
Neste caso, o MMC (8; 12) = 23 * 3 = 24.
À primeira vista pode parecer complicado, mas o que foi feito foi, basicamente, dividir os números desejados pelo menor valor comum a eles: o dois. Após, repetiu-se o procedimento com os resultados (4; 6).
Obtidos os números 2 e 3, realizou-se novamente a divisão, contudo apenas com o primeiro elemento, conservando-se aquele que não é comum (no caso, o 3). Uma vez completamente fatorado o primeiro termo, prosseguiu-se com a fatoração do 3.
Veja também:
Propriedades básicas do MMC
- O MMC de dois números primos entre si é o produto deles;
- Quando houver apenas dois números e o maior deles for divisível pelo menor, o MMC entre eles é o próprio número maior;
- Multiplicando ou dividindo dois números por um outro número diferente de zero, o MMC aparece multiplicado ou dividido por esse outro;
- Dividindo-se o MMC de dois números pelo MDC deles, o quociente obtido é igual ao produto de dois números primos entre si;
- Multiplicando-se o MMC de dois números pelo MDC deles, o resultado obtido é o produto desses números.
MMC de 2 e 4
Aplicando as propriedades acima indicadas, podemos facilmente concluir que o mínimo multiplicador entre 2; 4 será o maior número deles, pois o 4, que é o maior número, é divisível pelo menor.
Múltiplos de 3
Para sabermos o múltiplo de um número, basta multiplicarmos por outro número. Observe, por exemplo, os múltiplos do número 3:
3 * 1 = 3
3 * 2 = 6
3 * 3 = 9
3 * 10 = 30
3 * 15 = 45
3 + 100 = 300
E assim por diante.
Regra prática para calcular MMC
Podemos calcular MMC entre números naturais de duas maneiras distintas:
A primeira delas é multiplicar os números desejados até que entre eles apareça o primeiro número comum. Por exemplo, para determinar o MMC dos números 12, 18 e 24:
12 = 12, 24, 36, 48, 60, 72, 84, 96, …
18 = 18, 36, 54, 72, 90, 108, 126, …
24 = 24, 48, 72, 96, 120, …
Assim, basta observar que o primeiro número comum verificado entre os algarismos desejados é 72. Logo, este é o mínimo múltiplo comum entre 12, 18 e 24.
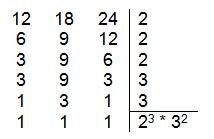
A segunda regra prática para calcular MMC também é bastante simples e relativamente mais rápida: basta fatorar ao mesmo tempo todos os números desejados. Pegando os mesmos números do caso anterior, temos:
Exercício de MMC
Agora que você já aprendeu a calcular MMC, responda abaixo as seguintes questões propostas:
1) Três atletas disputam um circuito. Ao dar a largada, todos saíram ao mesmo tempo, do mesmo ponto e no mesmo sentido. O primeiro atleta realizou o percurso em 40 segundos, o segundo, em 36 segundos, e o terceiro, em 30 segundos.
Com base nessas informações, responda:
- Depois de quanto tempo os três atletas irão se reencontrar novamente ponto de partida, pela primeira vez?
- Quantas voltas cada atleta terá completado?
(A) 5 minutos, 10 voltas, 11 voltas e 13 voltas.
(B) 6 minutos, 9 voltas, 10 voltas e 12 voltas.
(C) 7 minutos, 10 voltas, 11 voltas e 12 voltas.
(D) 8 minutos, 8 voltas, 9 voltas e 10 voltas.
(E) 9 minutos, 9 voltas, 11 voltas e 12 voltas.
Resolução:
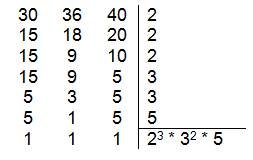
Realizando o MMC entre o tempo de cada ciclista:
MMC = 8 * 9 * 5 = 360 segundos (6 minutos).
Assim, o menor tempo em que os três se encontrarão novamente no ponto de partida é 6 minutos.
Por simples eliminação das alternativas já é possível perceber que a alternativa correta é a letra B.
Caso precisássemos encontrar o número de voltas dos atletas, basta dividir os seis minutos pelo tempo que cada um levava para dar uma volta completa.
Assim:
1º atleta: 360 / 40 = 9 voltas
2º atleta: 360 / 36 = 10 voltas
3º atleta: 300 / 30 = 12 voltas.
Logo, resposta: letra B.
Calculadora MMC
A calculadora de MMC é de simples uso e poderá responder questões rápidas. Após introduzir até 3 números, a calculadora mostrará logo abaixo o resultado do cálculo do MMC.
| [xyz-ihs snippet=”MMC”] |