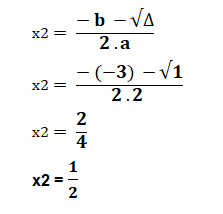Equação de Segundo Grau: Fórmulas e Exercícios
Neste artigo iremos introduzir alguns conceitos sobre a equação de segundo grau. Primeiramente, a equação de segundo grau pode ser definida como uma equação matemática que apresenta duas incógnitas denominadas x uma incógnita apresenta grau 1 e a outra de grau 2.
Entendo o que é uma equação de segundo grau
Dessa forma, denominamos de equação do segundo grau as equações do seguinte tipo ax² + bx + c = 0 com a, b e c pertencentes aos números 
Reais e, além disso, a deve ser diferente de 0.
Os parâmetros da equação do segundo grau são:
a se refere ao coeficiente principal;
b se refere ao coeficiente secundário,
c se refere ao termo independente.
Veja o exemplo de uma equação de segundo grau:
3x² + 2x + 3 = 0
Observe o grau 2 na primeira incógnita x.
Denominamos anteriormente que a, b e c são coeficientes da equação, neste caso o coeficiente a tem valor igual a 3; o coeficiente b é igual a 2 e o coeficiente do termo independente c é igual a 3. Além disso, a é sempre coeficiente de x², b é sempre coeficiente de x e c é sempre coeficiente do termo independente.
Observe outros exemplos de equações de segundo grau e o valor de seus coeficientes:
- 4x² + 2x + 1 = 0é uma equação do segundo grau, com a = 4, b = 2, c = 1;
- 2x² – x – 3 = 0é uma equação do segundo grau, com a = 2, b = –1, c = –3 .
- 7x² – 6x = 0é uma equação do segundo grau, com a = 7, b = –6, c = 0.
- 10x² – 5 = 0é uma equação do segundo grau, com a = 10, b = 0, c = –5.
Para a resolução de uma equação de segundo grau (ou seja, descobrir o valor de x) utilizamos a fórmula de Bhaskara. Usando essa fórmula podemos obter dois valores para a incógnita x.
Fórmula de Bhaskara
A fórmula de Bhaskara é a seguinte:
Sendo que ∆ pode ser calculado pela seguinte fórmula:
∆ = b ² – 4 . a . c
Δ pode apresentar os seguintes valores:
Se Δ for maior que 0 então a equação admite várias soluções em R.
Se Δ for igual a 0 então a equação admite uma única solução em R.
Se Δ for menor que 0, ou seja, Δ for negativo, a equação não admite solução em R
Resolvendo Equação de 2° grau
Para resolver a equação do 2° grau é necessário que encontremos as raízes da equação. Essas raízes são valores que quando substituímos nas incógnitas x tornam a sentença verdadeira e igual a zero. Dessa forma, as raízes da equação formam o conjunto solução da equação de segundo grau.
Portanto, as soluções da equação do segundo grau são chamadas de raízes da equação, ou seja, os valores possíveis de x e são apresentadas de forma separadas por x1 e x2. Onde:
Utilizando o que foi descrito até agora observe o seguinte exemplo para resolução de equação de segundo grau:
2 x² – 3 x + 1 = 0
a = 2; b = -3 e c = 1
∆ = b ² – 4 . a . c
∆ = (-3)² – 4 x 2 x 1
∆ = 9 – 8
∆ = 1
x1 = 4/4
x1 = 1
Portanto, a solução da equação 2 x² – 3 x + 1 = 0 é: S = { 1; ½ }
Exercícios
(OBEMEP) A partir da formula de Bhaskara, observando o modelo abaixo, calcule as raízes de cada uma das equações que seguem.
2x² + 2x − 4 = 0
Tem-se ∆ = (2)² − 4 · 2 · (−4) = 4 + 32 = 36 e, portanto, as raízes s˜ao: Daí, √∆ = 6 e
Logo, S = {−2, 1}.
a) x² − 7x + 6 = 0
b) x² − 5x + 4 = 0
c) 2x² + 1x − 10 = 0
E aí, conseguiu entender? Tente utilizar a fórmula de Baskhara com outras equações e nos conte como se saiu!
E, bons estudos!
Confira outros assuntos!
Como Calcular a Área de Figuras Geométricas: Fórmulas e Exemplos
O cálculo da área de figuras geométricas é uma das habilidades matemáticas fundamentais, tanto em ambientes acadêmicos quanto na vida…
Calcule as Potências 5 Elevado a 3 (5³): Fórmulas e Exemplos
No universo da matemática, as potências desempenham um papel central e fundamental no entendimento de uma variedade de conceitos e…
Dominando os Cálculos Matemáticos: Dicas Eficientes
Dominar os cálculos matemáticos é essencial para o sucesso em diversos campos acadêmicos e profissionais. Seja você um estudante em…
Gostou do artigo?
Avalie, compartilhe com seus amigos. Não esqueça de deixar sua opinião, contar sua experiencia sobre a equação do 2 grau.
