Produtos Notáveis e Fatoração: Exercícios e Exemplos
Os produtos notáveis são expressões algébricas que costumam aparecer frequentemente e elas são usadas na fatoração de polinômios. Confira aqui exemplos de fatoração e produtos notáveis. Aprenda de maneira simples!
O conteúdo estudado na Fatoração está ligado com a reunião de técnicas de transformação de subtração ou soma de variados termos de um produto. Em outras palavras:
| Definição: A Fatoração é o ato de transformação de uma soma ou de uma diferença entre duas ou mais parcelas como produto de dois (ou até mais) fatores. |
Fatoração
Fator Comum: ax+bx=x (a+b)
A expressão mais básica da fatoração é o Fator Comum ax+ay=a (x+y). Nele, devemos encontrar um fator que há nas respectivas expressões algébricas. Através deste fator comum, podemos simplificar a expressão fatorada.
Exemplo 1: Para fatorarmos a seguinte expressão (3x²-6x), devemos encontrar o Máximo divisor comum e, logo depois, encontrar o Fator comum. Temos assim:
3x²-6x = 3x (x-2)
Exemplo 2: Para fatorarmos a seguinte expressão (5x+5y), devemos deixar o ‘5’ em evidência, uma vez que o mesmo é o fator comum da expressão inicial. Assim, podemos obter a seguinte expressão aritmética:
5x+5y=5 (x+y).
Agrupamento: ax + bx + ay + by = (a + b)(x + y)
O agrupamento é um tipo de fatoração onde podemos agrupar dois fatores comuns, formando uma nova expressão algébrica. Por exemplo, na expressão ax + bx + ay + by, colocamos em evidencia o a e o b, como fizemos na etapa de Fator comum. Feito isso, acharemos ainda mais um Fator comum, que será o x e o y. Teremos então que:
ax + bx + ay + by =a (x+y)+b (x+y)= (a + b)(x + y)
Exemplo: 6x²-4ax – 9bx+6ab = 2x (3x-2a) – 3b (3x- 2a)
(3x-2a) (2x-3b)
Diferença de dois quadrados
Basicamente, a diferença de dois quadrados é exatamente igual ao produto da soma pela diferença, em outras palavras:
Produtos Notáveis
Os produtos notáveis são multiplicações que se destacam na aritmética. Isso é dado ao fato de as mesmas serem muito frequentemente utilizadas.
Quadrado da soma de dois termos
Conforme podemos notar na representação a seguir, o a se denomina como primeiro termo e b como segundo termo. Assim, temos que:
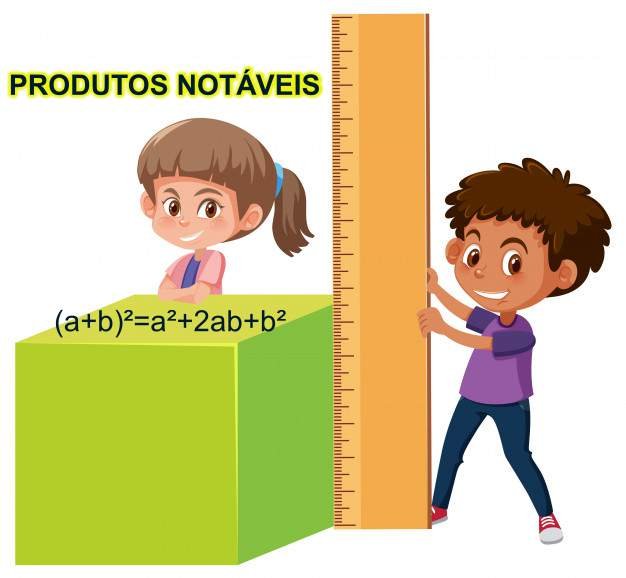
(a+b)²=a²+2ab+b²
“O quadrado da soma de dois termos é igual ao quadrado do primeiro termo, mais duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.”
Vídeo produtos notáveis: Exemples práticos
O quadrado da diferença de dois termos
Assim como anteriormente, na representação a seguir, o a se denomina como primeiro termo e b como segundo termo. Assim, temos que:
(a + b)² = a² – 2ab + b²
“O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo, menos duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo. ”
Produto da Soma pela diferença de dois termos
No caso de termos o produto da soma pela diferença de dois termos, é possível que transformemos numa diferença de quadrados, como podemos observar a seguir.
(a + b)(a – b)= a² – b²
“O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo.”
Triangulo de Pascal
O chamado triangulo de pascal é um triangulo infinito e simétrico, com seus lados esquerdo e direito sempre possuindo o número 1. A cada linha, o valor é correspondente a um número a mais que na anterior, possuindo também variadas propriedades que permitem construir a simetria do triangulo.
Veja a seguir algumas das propriedades.
- Uma das propriedades corresponde à soma dos elementos de cada uma das linhas. Ou seja, a soma de todos os números de uma determinada linha é correspondente a 2 elevado ao número associado a linha. Como, por exemplo, o 2³, onde ele aparece 3 vezes, obtemos assim:
Gostou do artigo?
Se gostou, entendeu um pouco mais sobre produtos notáveis e fatoração, compartilhe! Avalie também!