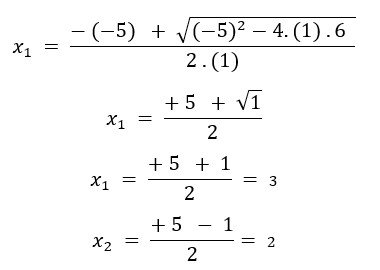Exercícios Equação do 2 grau: Resolução, Lista de Exercícios PDF
No ensino fundamental conhecemos a equação do 2º grau, no inicio parece complicada, mas para isso veja qui exercícios equação do 2 grau que te possibilitar entender melhor os tipos de problemas encontrados na solução das equações do segundo grau.
Hoje vamos conhecer alguns dos principais modelos de exercícios relativos a equação de segundo grau presente em provas, exames, vestibulares e concursos. Para isso separamos em três categorias: encontrar a equação de segundo grau equivalente a um problema , achar as raízes da equação de segundo grau e sistemas completos que consistem na junção dos dois últimos.
Exercícios equação do 2 grau
Confira exercícios equação do 2 grau e a respectiva resolução dos problemas. Veja também exercícios equação do 2 grau com gabarito em pdf.
Problemas do tipo A: encontrar a equação de segundo grau de um problema
Os problemas e exercícios do tipo A são o mais simples de serem resolvidos. Veja dois exemplos à seguir.
Exercícios equação do 2 grau Exemplo 1:
Se você multiplicar um número X pelo mesmo número real X e do resultado da multiplicação subtrair 20, você vai obter o óctuplo de X.
Qual a equação de segundo grau da questão?
Resolução
X é a variável da questão e quando multiplicamos X . X temos X².
Depois de subtrair 20 de X² temos:
X²- 20
Agora temos a parte: “obter o óctuplo de X” que em outra palavras significa é igual a. Assim, como resultado final, temos:
X²- 20 = 8X
Caso desejarmos podemos reescrever da seguinte forma:
X²- 8X – 20 = 0
Exercícios equação do 2 grau Exemplo 2:
Joaquim tem um negócio de reparo de peças. O custo de operação fixo de cada dia é 100 reais. O custo de cada peça depende da disponibilidade e pode ser calculado como o valor da peça ao quadrado. O valor que cobra para cada reparo é 5 vezes o valor da peça. Qual a equação que faz com que o negócio de Joaquim não seja nem lucrativo nem tenha prejuízo.
Resolução
Tudo que é custo vamos ter valor negativo. Assim o custo fixo é -100 e o custo de cada peça é -X².
Tudo que é venda vamos ter como valor positivo. Assim o total de venda é 5X.
Juntando tudo em uma única equação, temos:
-X²+ 5X – 100
Porém, falta dizer que queremos encontrar quando não tenha lucro nem prejuízo, ou seja, tudo isso é igual a 0, ficando assim:
-X²+ 5X – 100 = 0
Problemas do tipo B: encontrar as raízes da equação de segundo grau
São os problemas mais comuns em exames ou provas de ensino médio. São simples de resolver e a principal dificuldade está em resolver alguns sistemas que não são muito amigáveis. Todos exercícios do tipo B consistem em seguir uma receita que é encontrar o Δ e depois encontrar as raízes.
Tudo isso pode ser feito aplicando a fórmula de Bháskara.
Fórmula de Bhaskara
Se a equação de segundo grau tiver soluções reais ela vai ter duas raízes: x1 e x2.
Lembrando também que o Δ é:
Δ= b²-4 .a .c
Vamos agora resolver um exemplo para você ficar com mais prática. Fique atento em cada passo que vamos apresentar a seguir.
Exemplo: Encontre a equação as raízes do sistema abaixo:
X²- 5X + 6 = 0
Resolução
Para ficar mais fácil vamos anotar que a=1; b=-5 e c=6. Substituindo na equação de Bhaskara podemos encontrar x1 e x2.
Como podemos ver a equação de segundo grau apresenta duas raízes reais: 2 e 3.
Problemas do tipo C: encontrar a equação e suas raízes
Consiste em um problema do tipo A junto com um do tipo B. Se você entendeu ambos anteriores não encontrará dificuldade alguma no exemplo abaixo.
Exemplo: Um vendedor vende frutas. Sua receita depende do número de frutas (T) em T2 e tem uma despesa variável 4T e uma fixa de 5.
Quantas frutas (T) ele precisa vender no mínimo para não ter prejuízo?
Resolução
A nossa equação de segundo grau fica:
T²- 4T – 5 = 0
Usando Bhaskara
Como podemos ver temos duas raízes porém precisamos que o valor seja positivo por se tratar de quantidade. Sendo assim o vendedor precisa vender 5 frutas no mínimo para não ter prejuízo.
Vídeo Exercícios equação do 2 grau
Teste seus conhecimentos com os exercícios equação do 2 grau, aplicando a formula de Bhaskara Lista em PDF.